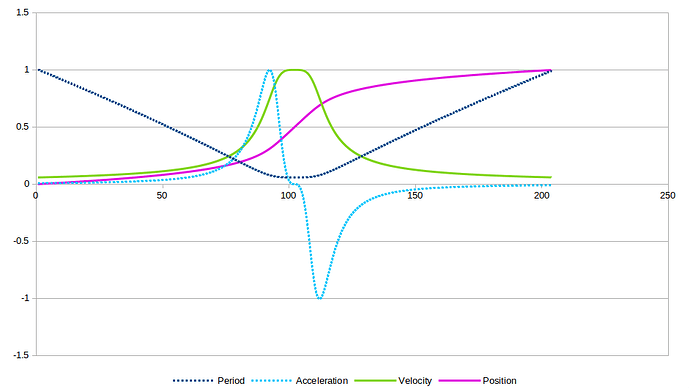
It looks like your graphs resemble theirs in all the ways that matter. Nice work! You are definitely doing something more interesting and sophisticated than I am. I went with a lookup table (and the minimum-length-move that imposes) in order to only have to solve a much simpler version of the problem.
I started from “jerk” (I’m still not sure how I feel about that derivative name, but I know I don’t like the next three  ) and worked my way up.
) and worked my way up.
The code I wrote for the table-generating half just walks the first two bumps of the “jerk” graph with real-world (experimentally determined) constants for things like the maximum acceleration I wanted to see and dumps them to a text file.
There is so much symmetry everywhere else in the problem that I just did the rest in Excel by, like, copy-pasting + negating and just keeping running sums for the next graph up the chain. 
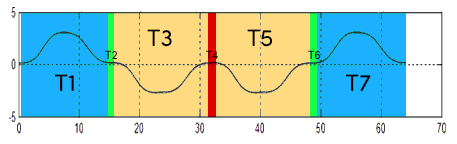
The key insight from the paper is that you can deal with the seven sections separately (during which the displacement monotonically increases):
T1: +jerk, acceleration ramp, velocity climb
T2: jerk = 0, acceleration max, velocity climb
T3: -jerk, deceleration ramp, velocity climb
T4: jerk = 0, acceleration = 0, velocity max
T5: -jerk, deceleration ramp, velocity fall
T6: jerk = 0, acceleration -max, velocity fall
T7: +jerk, acceleration ramp, velocity fall
If you’re willing to use a lookup table, all you really need to capture is periods T1 through T3.
For T4 you can hold at your favorite max speed for as long as you like (velocity, acceleration, and jerk will all still be continuous). You could also safely hold on T2 and T6, but I’d rather reach peak velocity as soon as possible.
Then, T5 through T7 are just the mirror image of T1-T3.
Because I’m not doing any math on the microcontroller–instead, just walking through the delay lookup table array–it does require that the move you’re making has at least as many steps as 2x the velocity ramp. So, for my preferred micro-stepping, I just tuned the length of the T1-T3 lookup table until it was a little under half a frame’s worth of movement. It may dwell at max velocity (T4) for a few extra milliseconds before it starts ramping down, but everything remains very smooth.
On the microcontroller, the whole table ended up compact enough that it can be shown here, inline:
static constexpr u16 move428[214] PROGMEM {
250,250,250,250,250,250,250,250,250,250,250,250,250,250,250,250,250,250,250,249,249,249,
249,249,249,249,248,248,248,247,247,247,246,246,245,245,244,244,243,243,242,241,240,240,
239,238,237,236,235,234,233,232,231,229,228,227,225,224,223,221,220,218,217,215,214,212,
211,209,207,206,204,202,201,199,197,196,194,192,190,189,187,185,184,182,180,179,177,175,
174,172,170,169,167,166,164,163,161,160,158,157,155,154,152,151,150,148,147,146,144,143,
142,141,139,138,137,136,135,134,133,132,131,130,128,127,127,126,125,124,123,122,121,120,
119,118,117,117,116,115,114,113,113,112,111,110,110,109,108,108,107,106,106,105,104,104,
103,102,102,101,101,100,100,99,99,98,98,97,97,96,96,96,95,95,94,94,94,93,93,93,92,92,92,
91,91,91,91,90,90,90,90,89,89,89,89,89,88,88,88,88,88,88,88,87,87,87,87,87,87,87,87,87,87,87,87,86
};
Since my table ended up 214 entries long for the initial acceleration ramp, I always need to ask for a move at least 2 x 214 steps long: half for the acceleration, half for the deceleration. (Otherwise the code falls back to a simple, fixed-delay move… which you can hear as a very different kind of stepping sound from across the room, hehe.)
So if you ask for, say, a 500 step move, it will walk through the delay table for the first 214 steps, use the final value in the table for (totalSteps - 2 * 214) = 72 consecutive steps, then walk backward through the table for the final 214 steps.
It’s such a simple scheme that you end up with the minimum-length move limitation, but being able to generate the table and implement the lookup so easily, it was worth it. The math’y code was a lot worse during my early prototyping, but once I recognized all the symmetry, I ended up with the longest (only?) formulas in my code being the first and third entries from equation (1) in the paper:
double T1(double t) { return jmax * sin2(k * (t - 0)); }
double T3(double t) { return -jmax * sin2(k * (t - t2)); }
After initially trying to implement the rest of the paper and deciding things were beginning to spiral out of control for my poor little Arduino, I took the simple route. It sounds like you made it farther than I did! I’m curious to hear your results.