Kodachrome Colors

cpixip · January 11, 2025, 2:12pm

I want to report on some investigations about Kodachrome 25 film stock. My primary intention is to create a virtual color checker “made” out of Kodachrome film stock.

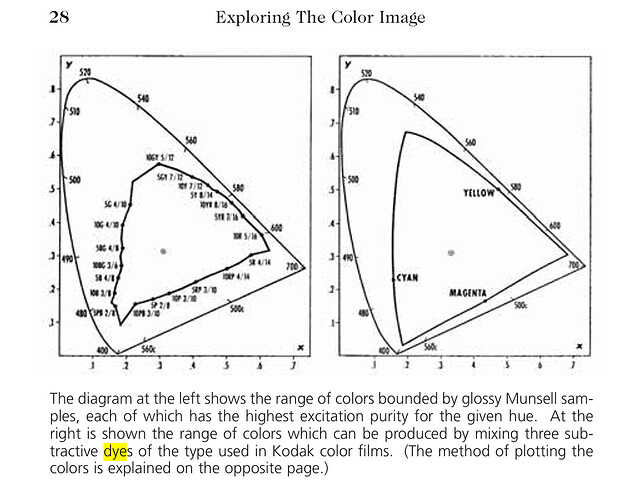
While doing this research, I stumbled over an internet page, “How Good Was Kodachrome?”, which is in part an interesting read. For starters, the page discusses the issue whether maximal color separation is a valid goal, or whether one should rather opt for overlapping filter channels (I support that later view).

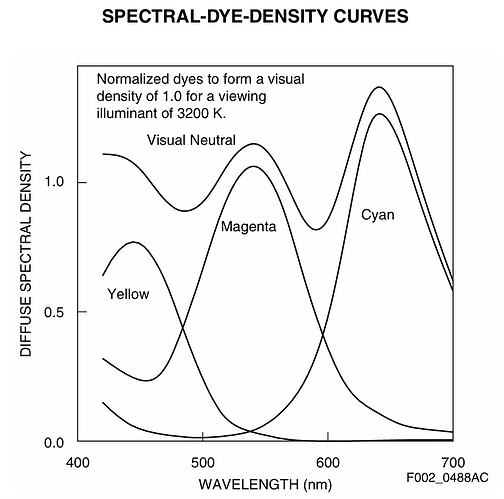
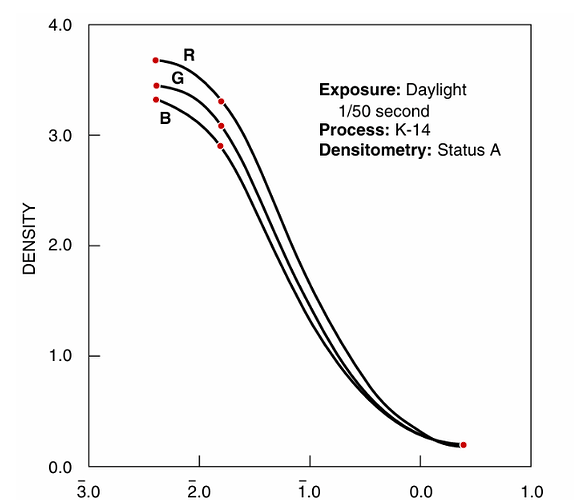
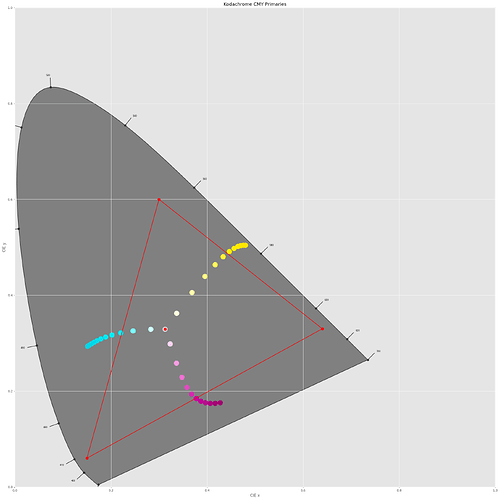
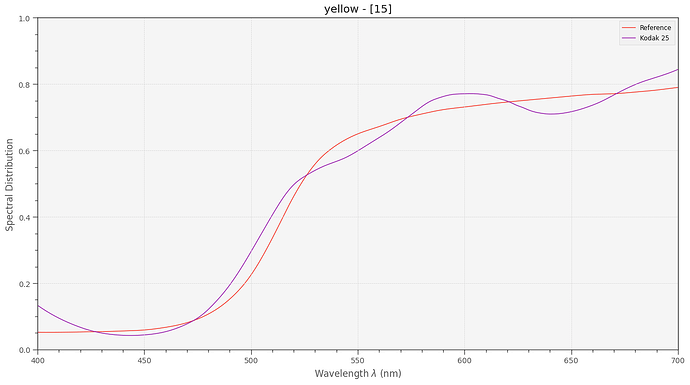
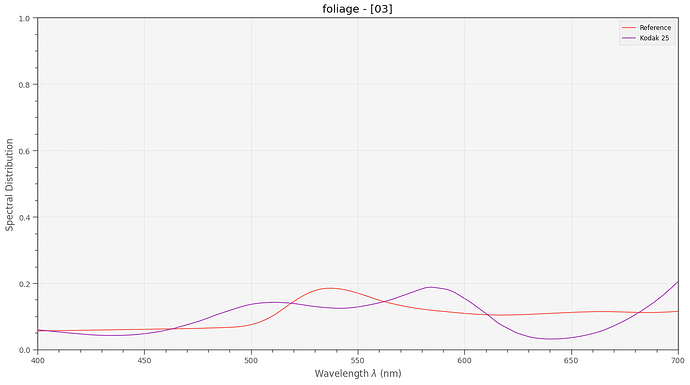
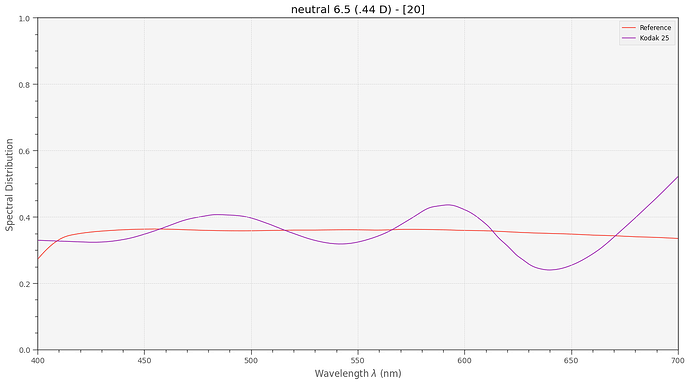
Anyway - I did the following experiment. From the Kodachrome 25 data sheet I took the spectral density curves of the yellow, magenta and cyan dye layers,

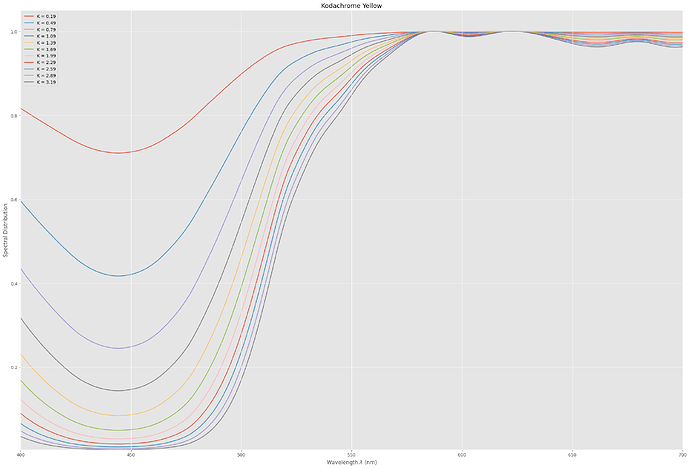
In order to arrive at a filter characteristc for each of these dye layers, I basically calculated 1.0 - d(lambda) (see below for an actual code segment). So the filter action of the yellow dye should yield a filter spectrum like this:

with equivalent handling of the magenta and cyan layers. In Python/colour science code, this is handled by the following code segment

    MagentaAbsorption = one - KodachromeM*scaleM
    CyanAbsorption    = one - KodachromeC*scaleC
    YellowAbsorption  = one - KodachromeY*scaleY

    totalAbsorption   = MagentaAbsorption*CyanAbsorption*YellowAbsorption

Here, KodachromeY is for example the spectrum of the yellow dye, scaleY is the density of the the yellow dye, and totalAbsorption the complete film absorption.

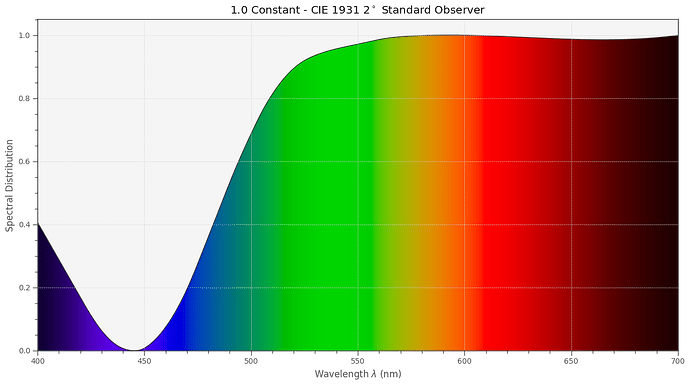
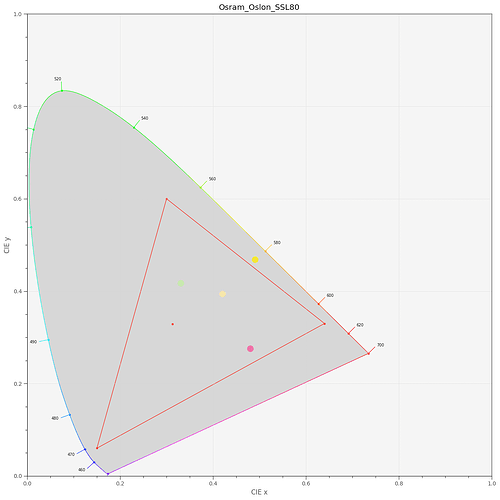
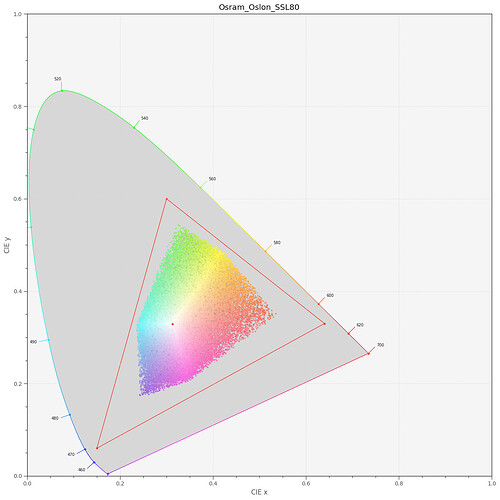
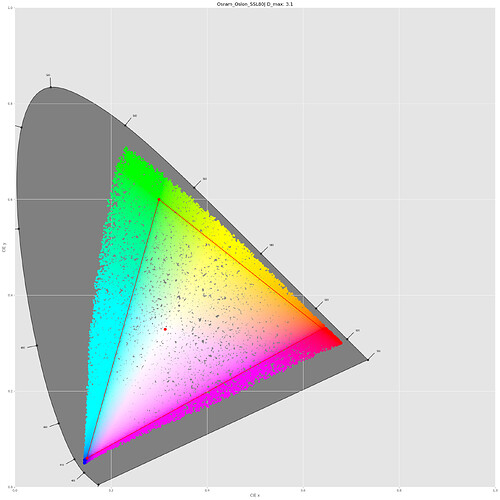
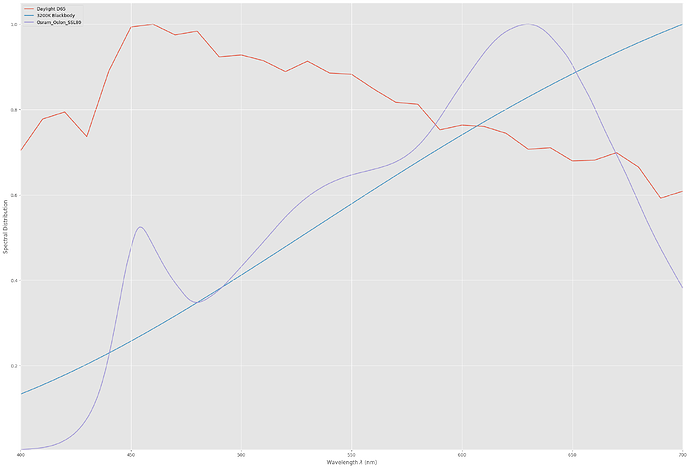
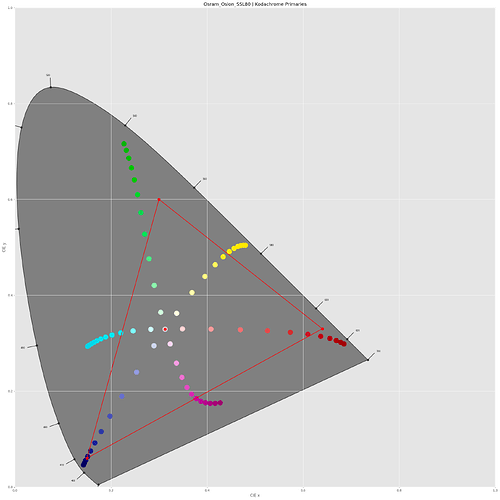
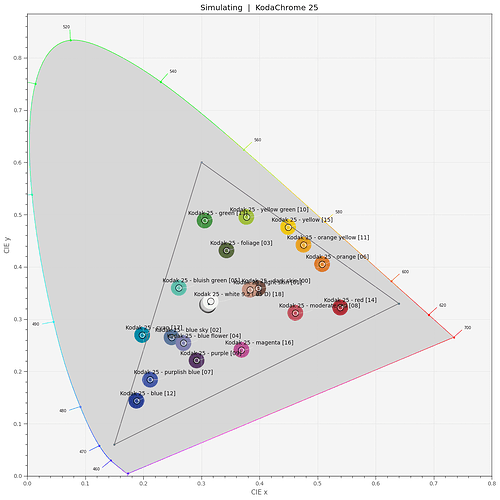
With this in place, I can check where the dye layers end up in a CIE-diagram. For this, I need to select a light source, I opted for my trusted Osram SSL80 whitelight LED:

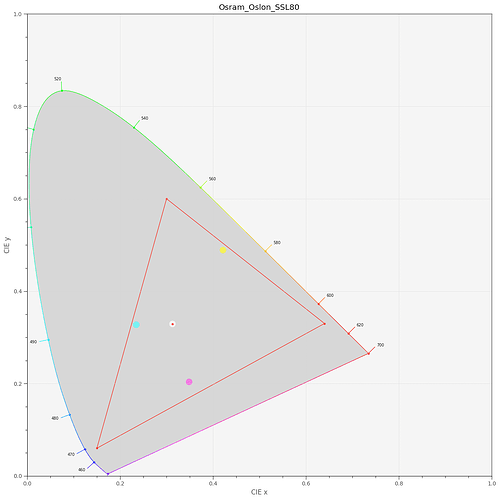
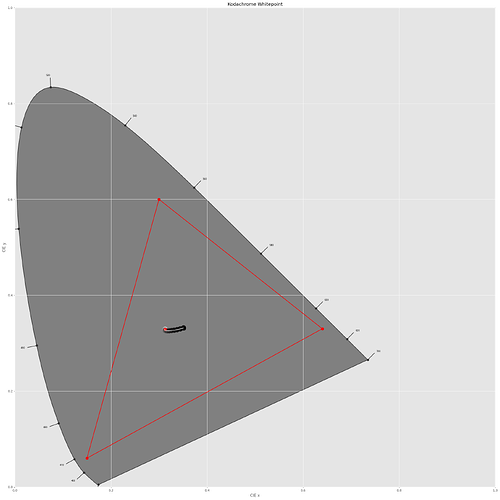
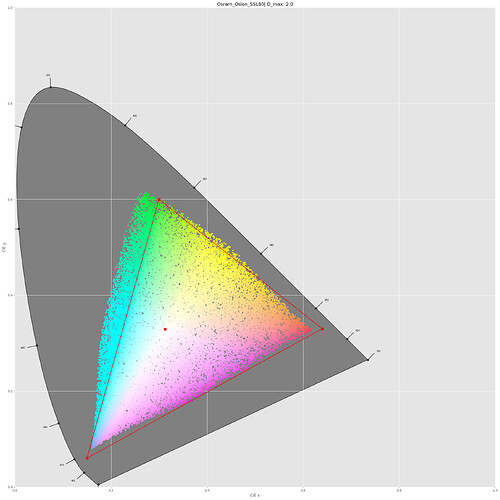
In the above diagram, the sRGB color gamut including its primaries is indicated by the red triangle. The yellow dye (yellow dot) is slightly out of the sRGB gamut, the two others (magenta and greenish dots) are within this color gamut. Of importance is the center dot - this is the position of the whitepoint - clearly, it’s off from the sRGB one (the small red center dot). So I guess I have to throw in a color space adaption transformation (CAT) here. I use the linear Bradford method (which is the same as recommended in the Adobe DNG-spec) and finally arrive at the following diagram:

Well, the whitepoints do match now and all Kodachrome 25 primaries have moved into the sRGB space!

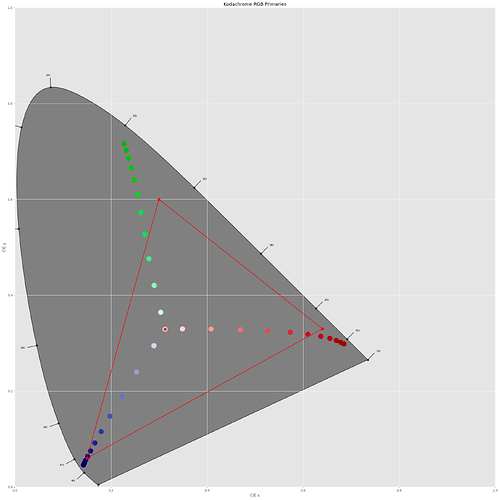
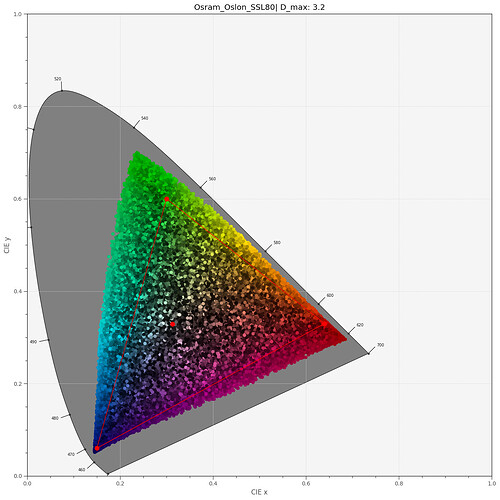
To get an idea of the total color gamut representable by the above dye spectra, I run a simulation of 50000 random combinations of the three dye spectra, basically picking random values for the scaleY, scaleM and scaleC amplitudes, keeping them in the range [0.0:1.0]. This is the result:

So it seems that all colors which are representable by a combination of Kodachrome 25 dye spectra easily fit into the sRGB color gamut. Frankly, I did not expect that.

I do not know whether my approach presented above is valid, but I do not see any obvious mistake. I take a virtual light source, pipe this light spectrum through yellow, magenta and cyan filter layers representing the dye layers and compute the resulting overall spectrum. This spectrum is converted into a XYZ color which in turn is mapped into the xy-diagrams above.

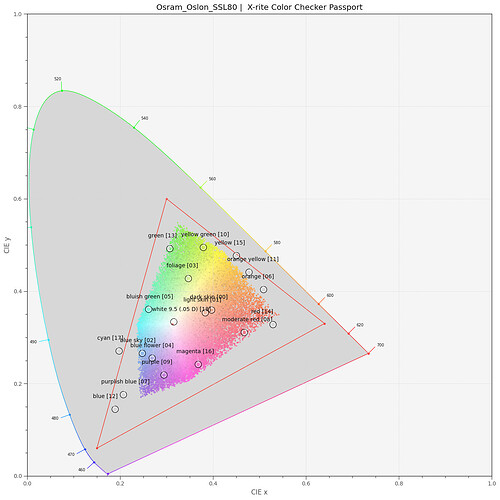
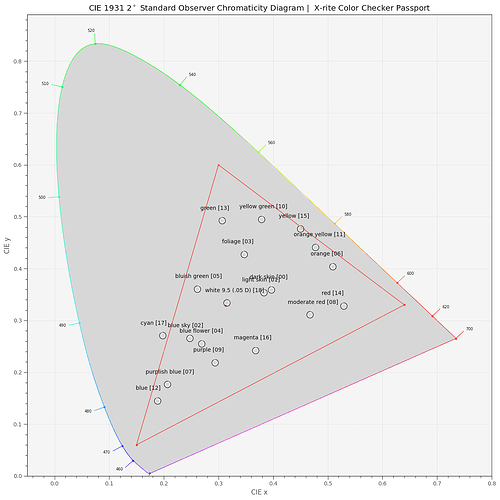
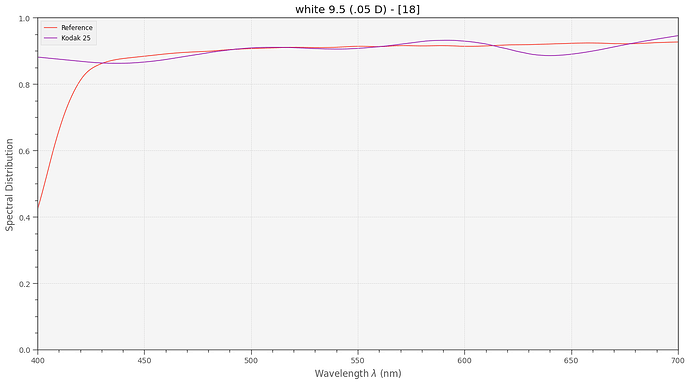
If this results is true, my actual project, namely creating a virtual Kodachrome 25 color checker, is not possible. Overlaying a standard color checker board,

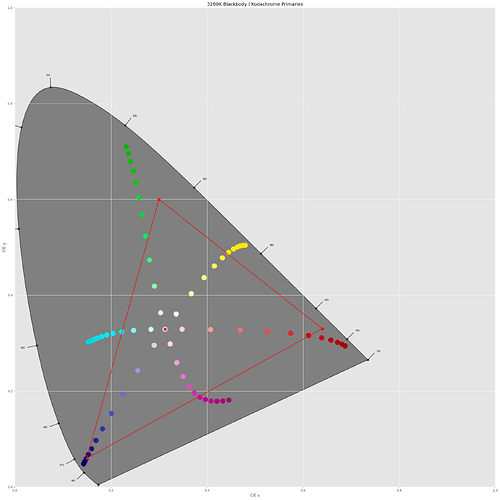
I can count 7 patches of the color checker for which a representation with Kodachrome 25 dyes seems impossible. These are mainly blue/cyan and yellow/orange/red colors. Note that the correlated color temperature (cct) of the SSL80 is 3212 K, which matches closely the illuminant of 3200 K cited in the Kodachrome 25 data sheet. The CRI of my (simulated) SSL80 is computed to be 97.286. A simluation with a real 3200 K blackbody radiator does not change the results.

EDIT: I think I interpreted the original Kodachrome 25 data wrong. First, it is noteworthy that the SDs given are not normalized - overlooked that. Also, I need to take into account that these are densities which can vary more than just in the interval [0:1]. Lastly, the mentioning of a “illuminant of 3200 K” in the data needs further investigation. Normally, SDs are not dependent on the illumination source. Please refer to later posts in this thread for further aspects.

PM490 · January 11, 2025, 4:33pm

Thank you for sharing your research, interesting link.

If I understand the findings correctly, my interpretation would be that Kodachrome + LED is unable to reach some of the targets (actually LED or 3200K blackbody radiator).

My perspective -if I interpret the findings correctly- is that if a color checker was filmed on Kodachrome those 7 patches would not be in the intended locations, would be somewhat shifted/shrunk in the direction of the white center.

However, creating a synthetic target showing the shifted/shrunk resulting locations of these (within the Kodachrome gamut) would be quite helpful, as it would allow the use of the Resolve Color Match function to adjust to best fit, stretching the surrounding colors on the film patches to the digital gamut patches.

To do so, I guess it would be necessary to (proportionally?) decrease the vector of spots in the vector where the gamut is limited.

Akin to what I am doing empirically with the synthetic targets derived from raw values (I will share the process to reach the values of the RGB mixer later).

npiegdon · January 11, 2025, 8:59pm

Yep, so long as you can measure the XYZ colors (normally with a photo spectrometer but in the synthetic case you’re starting with those) across a representative sample of the gamut, you’ll have something quite useful.

I’m not sure how you teach Resolve about new color targets though. Is that an open/extensible format? The way that I do it with the IT8 target is to convert the resulting ICC (from Argyll) into a standard LUT file that Resolve knows how to use. It’s like doing the Color Match step outside of Resolve and just importing the final result. It amounts to the same thing: instead of a Color Match node you just stick a LUT node in the same place instead.

Or, when you suggested “proportionally”, did you mean to use the same/existing target choice in Resolve and just have it “stretch” the colors out farther to the original values in the target? You’d probably get something oversaturated, but if you did it right (proportionally, like you said), would it just be a matter of turning the saturation back down a little?

PM490 · January 11, 2025, 9:56pm

The later.
In real world, a color target will be shown within the kodachrome gamut (off the location expected). The purpose of the color match is to bring the representation of the targets to the digital gamut location.

In the synthetic world, the idea is to represent the vector of that color target where it would have been depicted in the kodachrome gamut, the Resolve color match function would then try to bring those to the corresponding location in the digital gamut.

npiegdon · January 12, 2025, 3:36am

It’s kind of remarkable how little there is to find on the Internet when you search for discussion about the size of various film gamuts.

The only thing I was able to find with something that looks like real measurements was this page where the “Kodachrome Family” (not sure how that fits in with “25,” etc.) cannot be completely represented in sRGB. They found that only 91% of Kodachrome’s colors could be represented (with the other 9% falling out of gamut).

The “Color Set Evaluations” section at the bottom of the page has the table. KK is Kodachrome. I was surprised to see that Ektachrome (“KT” in the table) appears to have a wider gamut by virtue of it always having a smaller representable percentage of colors in every color space than Kodachrome’s.

cpixip · January 12, 2025, 9:12am

Yep. Just for reference, let me insert here a few bits of information I found while searching the internet for some further enlightment.

I found a better description of the spectral dye density data in one of Kodak’s other publications:

The spectral-dye-density curves indicate the total absorption by each color dye measured at a particular wavelength of light and the visual neutral density (at 1.0) of the combined layers measured at the same wavelengths.

Spectral-dye-density curves for reversal and print films represent dyes normalized to form a visual neutral density of 1.0 for a specified viewing and measuring illuminant. Films which are generally viewed by projection are measured with light having a color temperature of 5400K. Color masked films have a curve that represents typical dye densities for a mid-scale neutral subject.

So these curves are not what I initially assumed they are. Which solves my initial confusion prompting me to start this thread in the first place.

Second, in the scanning community, there seems to be some hype about Kodachrome slide scans coming out too blueish. In his “Reproduction of Colour” book RWG Hunt stated (p229):

When the viewing conditions consist of projection by tungsten light in a darkened room, the light form the projectors appears yellowish, and therefore to obtain results that appear grey the picture has to be slightly bluish; this is why the curves of Fig. 14.9(a)… are not even approximately coincident, the blue densities being lower than, and the red densities higher than, the green densities, in order to produce the bluish result required.

Here’s another find, from an old publication from ARRI comparing digital output devices (DLP and CRT) with classical film projection (EDIT: removed the links):

Motion picture print film has a wider gamut in the darker colors, especially in the blue and cyan hues. DLP and CRT monitor can produce more saturated bright colors in the red, green, and blue hues, but they cannot reproduce the yellow of print film, although the DLP does a better job than the CRT.

In essence, the authors state that you can never achieve with current digital display technology a display comparable to the projection of print film, at least in certain color ranges. Basically, this boils down to print film being a subtractive process, while digital display technology is based on additive color.

It would be great if other forum member can share/add additional information on Kodachrome or, generally, the difference between analog and digital media.

npiegdon · January 12, 2025, 9:43am

Those last two arri links seem to be behind some sort of authentication prompt. Do you know where/how to log in to read them? Even going to the subdomain root still makes the prompt appear.

That’s pretty cool engineering to have the film work in tandem with the light source (back when you could count on all users having the same color temperature), but it does throw a bit of a wrench into the gears. I suppose our to-taste white balance tweaking is a stand-in for pulling that wrench back out.

This also means simple response curves and 2D chromaticity diagrams aren’t enough to really simulate everything. If there was already scant data for this stuff, what do you suppose the chances are of getting our hands on a 3D gamut volume for Kodachrome?

PM490 · January 12, 2025, 11:00am

Interesting. The results of the synthetic color target experiment are also blueish, which I had attributed to inaccuracies in the creation of the target, but according to the references, that is the correct color. Cool.

cpixip · January 12, 2025, 11:00am

I am sorry - I have changed the above post. Was not aware that this is restricted material and did not check the links before posting. It’s been years (the document is from 2005) since I read that.

To summarize again what is discussed there: basically, there are quite large parts of the color gamut of print film which are hard to transcribe into a digital media format. The main reason is that film is a subtractive technology while digital media an additive one.

Which brings me to this:

Yep, has always been the case. In fact, Bruce Lindbloom has a nice animation for this.

Note that I am not doing in my simulations by basing them on “simple response curves and 2D chromaticity diagrams”. These simulations are usually carried out in spectral space, which is a function space (dim = infinite). Only where appropriate, XYZ coordinates are used (dim = 3). I am using chromaticity diagrams only for a quick and easy visualization; the input here is usually XYZ which is converted down to xy (dim = 2) for display purposes.

Using the full spectra data is mandatory to capture illumination specifics as well as modelling metamers correctly, for starters. As soon as you have condensed down the wild variation possible in any spectra to a few numbers (dim = 3 to 12), with 3 corresponding to classical RGB sensors and 12 to many multi-spectral cameras, you loose some precision.

Well, if the SD-curves cited above from the Kodak data sheet are somewhat close to the real curves of the material, the 3D gamut volume of Kodachrome can be calculated. Basically in the same way as I did above. Only with the correct input.

My problem is that my trivial interpretation of the data (being simple absorption SDs from which I can derive the transmission spectrum as described above) is obviously not valid. I probably have to throw in some log-transformation to get from the absorption SDs to transmittance data. Something like I_out(lamba) = I_in(lambda) * 10**(-A(lambda)). Will check this as next step. If that does not work out correctly, I have to attend the “for a viewing illuminant of 3200 K” remark in the above diagram. That could indicate that the spectra are not referenced to standard illuminant E but to something like D32. If so, I would need to rescale the data curves from the data sheet. I guess that’s at least the plan for the next days/weeks. It might not work out, we will see.