Following a suggestion from Pablo (@PM490), I want to start here a thread about color. For this, I have to resurect quite a few old JupyterLab notebooks. I’ll try not to say too much nonsense, but bear with me if I’m wrong.
In this initial post, I will talk a little about illumination sources. Part2 will talk about human color perception, part3 will discuss the response of digital cameras and how to optimize these.
I use for the diagrams extensively the Python Colour package - which is both intimidating and powerful, plus my own software ramblings.
Anyway. Human color perception is a complicated and not yet fully understood process. It is based on “light”, which is simply electromagnetic radiation in a certain, very small band. Specifically, human color vision is more or less limited to the range spanning 380 to 700 nanometers.
Within that small section of the electromagnetic spectrum, object surfaces have a characteristic foot print which in the end leads to the perception of a certain color by humans. As a side note: most other animal’s vision work in the same or a similar range of the spectrum, but feature occationally more different photoreceptors than humans: we have only three different ones available. And that will play a role later in this text.
Now, every single surface of an object reacts differently to the incoming light. Technically, this is described by a spectrum - which gives for every wavelength the amount of incoming light reflected back to the observer. The variance in these spectra creates the perception of different colors.
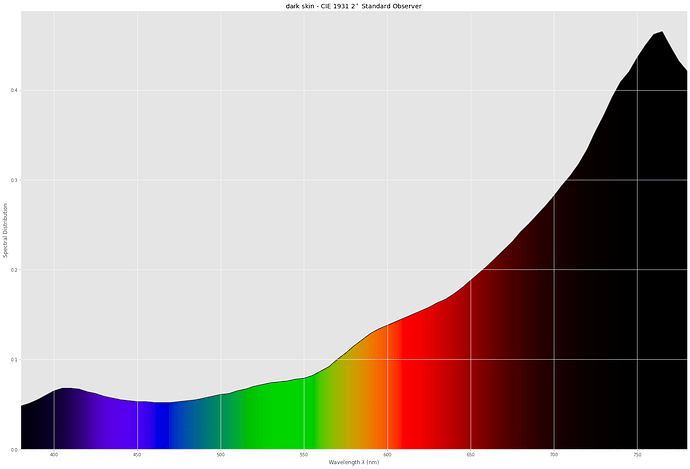
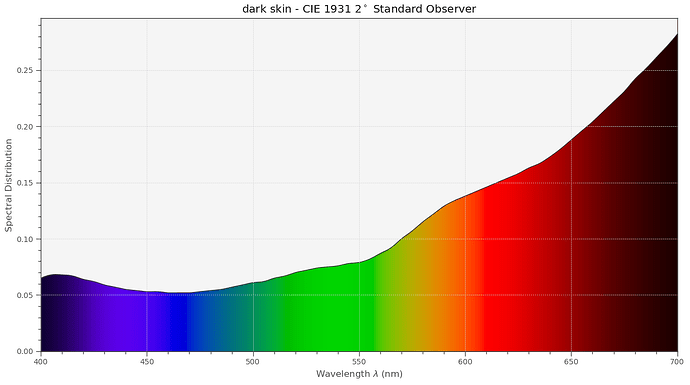
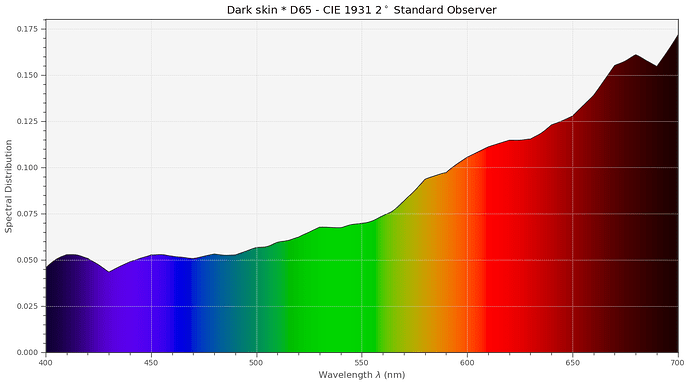
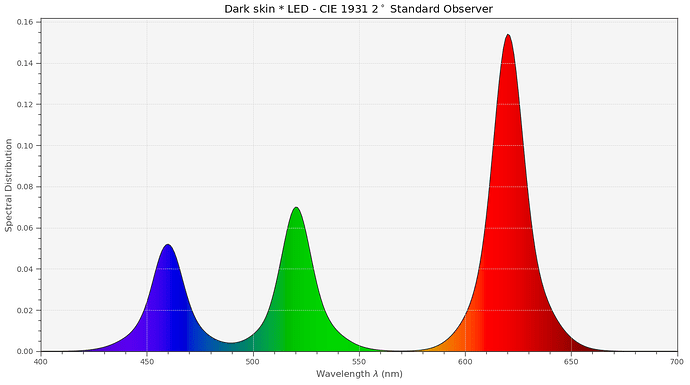
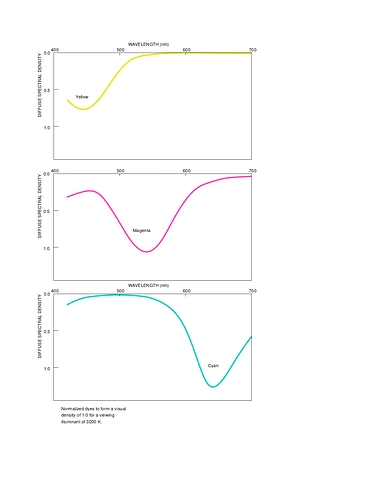
For example, this is how much dark skin is attentuating incoming light:
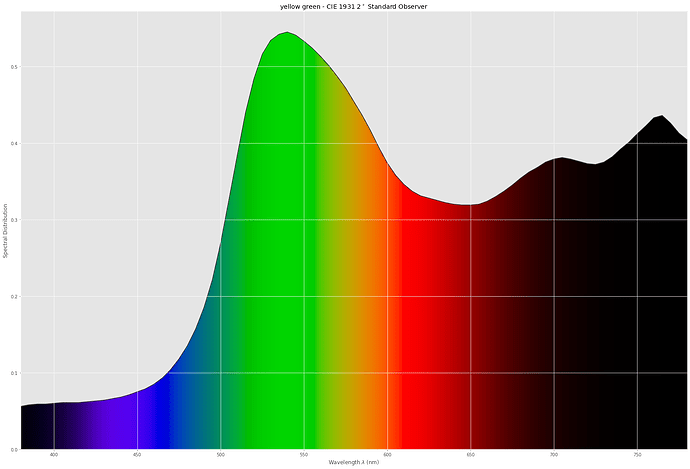
and this here is a spectrum of the green leave with a yellow tint:
How do we get from such a spectrum to the color perception a human observer would have? Well, for this, we need to talk a little bit about physics for a moment. The first thing to consider: light sources.
Light sources are radiation sources emitting light in some range of the electromagnetic spectrum.
Nature evolved all seeing beings in such a way that they are responsive to this little spectrum band. The reason is simple: that’s were sufficient light intensity is available by the sun and scattered light.
Not only do surfaces have spectra, but lightsources as well. Bright daylight is different from afternoon daylight or the light of a candle.
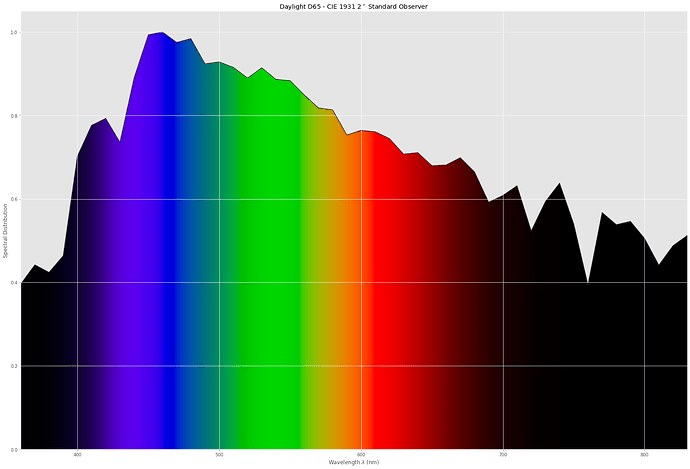
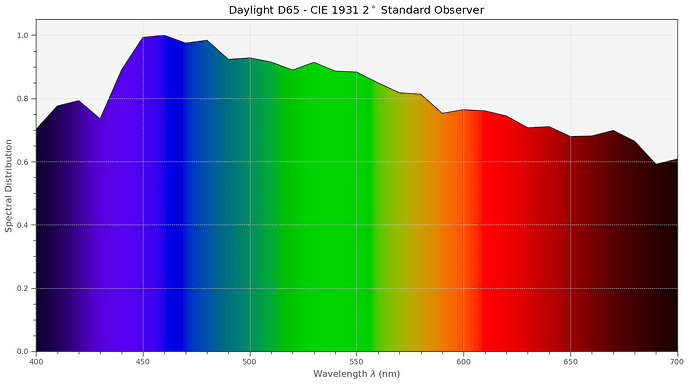
In fact, there is standard illumination defined which corresponds to “sunny, clouded day” - it is called illuminant D65 and is traditionally used when checking the colors in the print industry, for example. It looks spectral-wise like this:
So in a normal daylight scene, the light which actually reaches the eye of our human observer is the product of the light source’s intensity multiplied by the amount of light reflected by the surface of the object we are looking at - at every single frequency of the spectrum.
So, we end up yet with another spectrum, the combination of the illumination and the surface spectrum. This spectrum is projected onto the retina of our virtual human observer. Here, there are three basic receptor types, with filter responses (yet another spectral function) somewhat similar to the Bayer-filter in our cameras.
(These filter responses are rather broad. And that has to something to do with efficient data compression. The goal of the evolution was to be as sensitive to important variations in the spectrum of a fruit, for example, as possible, with the least amount of necessary hardware. One way to achieve this technically is principle component analysis (PCA). Basically, that is a transformation from, say, a complicated function to a less complicated one. The less complicated one is composed of functions becoming more and more complicated. In our case, the simplest approximation would be the constant average signal strength, the next complicated function would have a single bump (instead of being constant like the first one), followed by a function featuring two bumps and so on. Both representations of of a spectra are equivalent. But if you are not interested in details, you can stop the PCA after the first few components. That’s what evolution has done: in our case, we have three types of photoreceptors, some other animals have less, some other animals more.)
Already at the level of the retina, an amazing amount of computations are performed. There’s a huge image compression happening. Our optical nerve which connects the retina with V1, the first computational vision component in the back of our brains, features only 800 000 to 2 000 000 nerves - all things we perceive visually has to flow through this modest amount of signal cables (the screen I am typing this on has 2 304 000 pixels). And these nerves do not feature HDMI-type transmission speeds…
For our purposes, we do not need to get into all this detail. In 1931, a reference human observer was borne - that is the standard reference mostly used in color science. Every color perceivable by human beings can be characterised by only three color values (XYZ), or, if the brightness does not matter, by only two variable (xy). To arrive for example at the Y-value of a specific surface color, all one has to do is to fold the combined “light source”-“surface” spectrum with an appropriate filter response. Apart from a little further detail: the chromatic adaption capability of the human visual system. In photographic terms, this is similar to setting the appropriate white balance for a scene. This processing step assures that the pages of a book look kind of white in daylight, but also when reading this book under candle light. Within the context of the simulations here, I am using as chromatic adaption transform (CAT) the “linear Bradford” transform. There exist a lot of others - from “von Kries” to “CAT16” - does not matter too much for our purposes. In the end, simulating how a human observer would see a scene boils down to a bunch of spectral filter operations, with the last one condensing down the many values of the spectrum to only three color values, plus a chromatic adaption step.
Coming back to illumination spectra, an important class of spectra is connected to the radiation a black body of a certain temperature emits. Take for example the sun in empty space. Or a Tungsten lamp. Or a candle. The spectrum of these light emitters are all very close to a black body radiator.
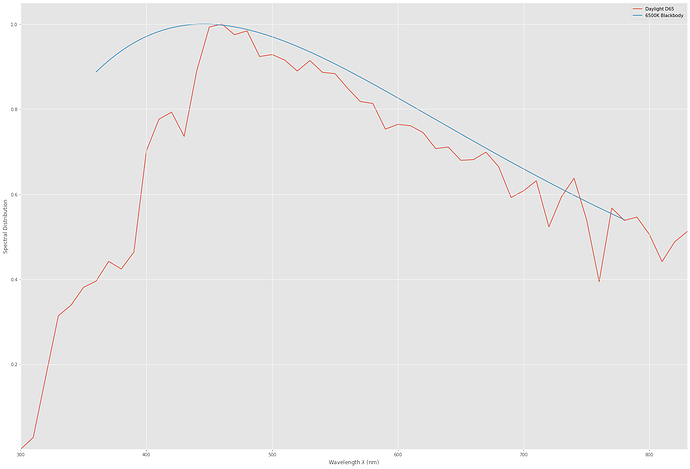
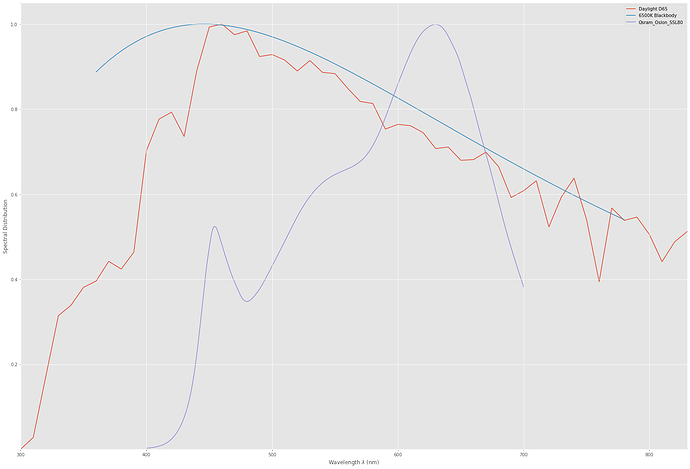
We can compare the radiation of a blackbody at 6500 K to the D65 spectrum:
Quite similar (the 6500 K is where the 65 of the D65 came from), but sligthy different.
Let’s see how a human observer would perceive a standard color checker illuminated by either D65 or the 6500 K blackbody radiator. For this simulation, the above sketched signal path (folding of illumination and surface spectra, filtering down to YXZ-values followed by a CAT)
Just a short explanation of this kind of display. Shown is the arrangement of the color checker’s patches. In the central part of each patch (“Inset”) the reference color is displayed how it should look ideally to a human observer. The remaining ring of each patch shows other data. In this case, the left half of each patch shows the result under D65 illumination, the right side what came out with the blackbody 6500 K illumination.
Besides the visual display, on the bottom there are some numerical values. Basically, for each rendering of the color checker, the color difference ΔE with the reference (the center CIE 1931 pathc) is computed. Generally, ΔE’s less than one are imperceptible, ΔE’s above one might be noticed by a human observer. The mean ΔE and the patches with the minimal and maximal deviation are listed for each test. The patch numbers are also displayed in the lower left corner of each patch.
Now, we see that there is no difference between D65 and CIE 1931 at all. That is because the reference illumination of the CIE 1931 is D65.
However, there is a tiny difference in color perception between the blackbody 6500K illumination and the standard observer.
Let’scheck the CRI of these illuminations:
D65: 99.999
blackbody 6500 K: 97.995
Indeed, our blackbody illumination features a slightly less CRI than the reference illumination (which should not really come as a surprise), but it is still rather high.
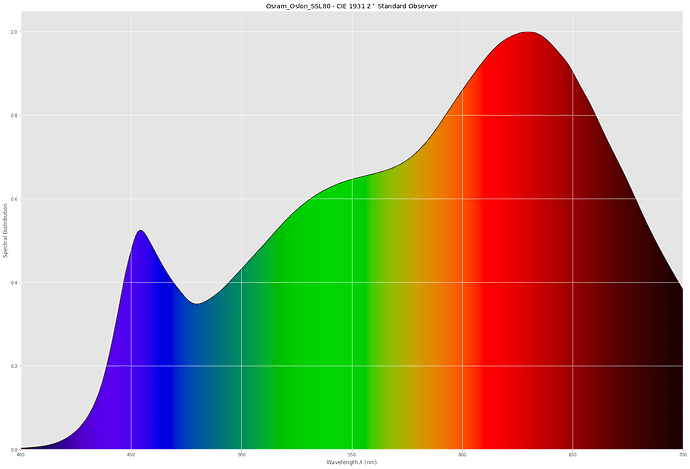
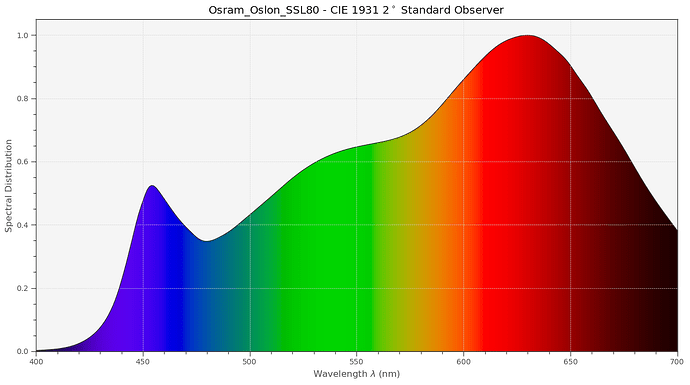
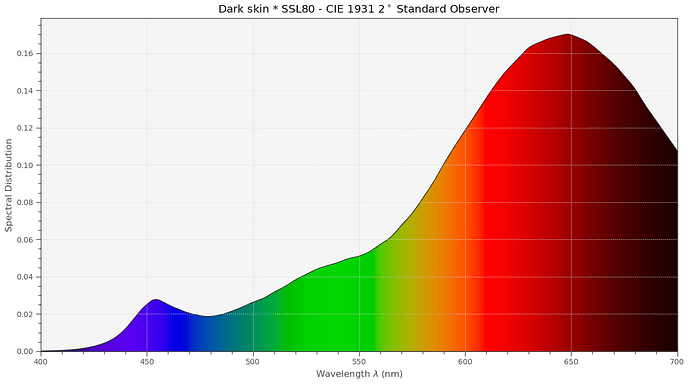
Now we are going to compare this to a whitelight LED (specifically, an Osram Oslon SSL80) which features the following spectrum, according to the data sheet:
And the CRI reported is at 97.286. Great!
But… let’s compare the Oslon spectra with the two other illumination spectras:
The LED spectrum does not look at all similar to our previous illuminations. How come it has such an high CRI?
Remember that we talked above about the chromatic adaptation (CAT) occurring in human color vision? That a book viewed in bright sunlight more or less looks the same when viewed by candle light? We included in our blackbody radiation already the idea of a temperature, in this case 6500 K. And that number, called correlated color temperature (cct) is an important characterisation for illumination purposes. So let’s calculate the ccts of our spectra:
D65: 6500.4
Blackbody 6500K: 6500.0
SSL80: 3212.0
So… - this solves the riddle somewhat. The cct of the SSL80 is quite different from our other two spectra. It’s closer to candle light than to daylight.
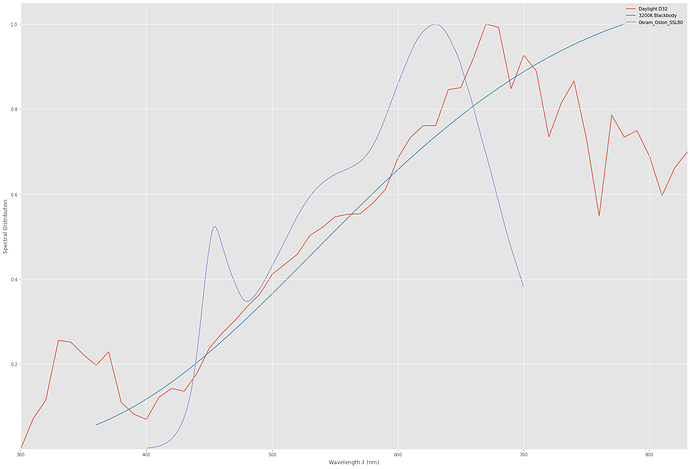
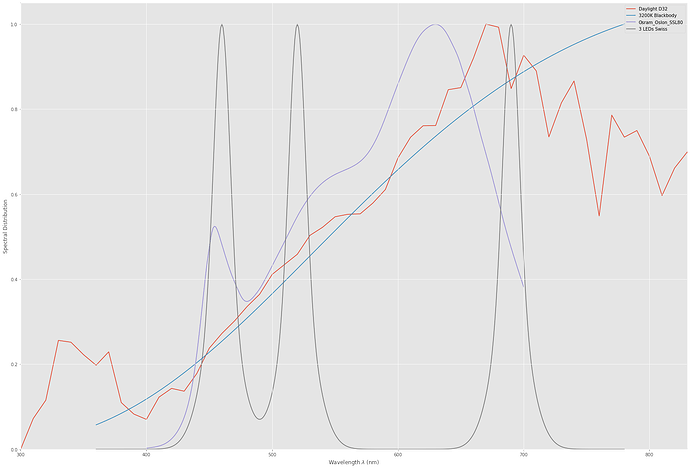
Let’s create a D32 (which is not really defined, but that’s another detail) and a blackbody 3200 K:
That looks much more similar spectral wise!
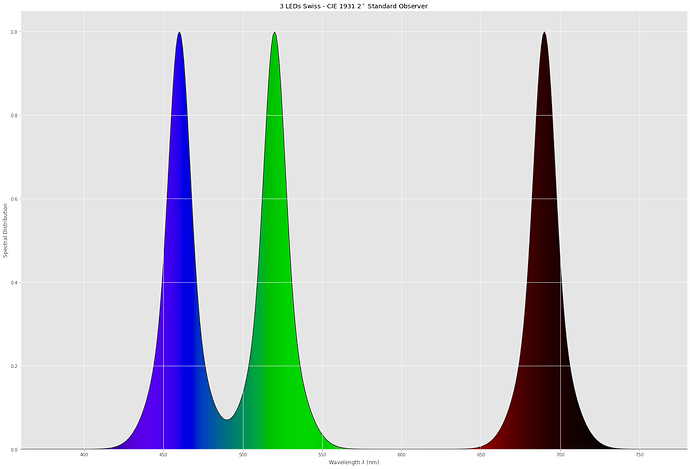
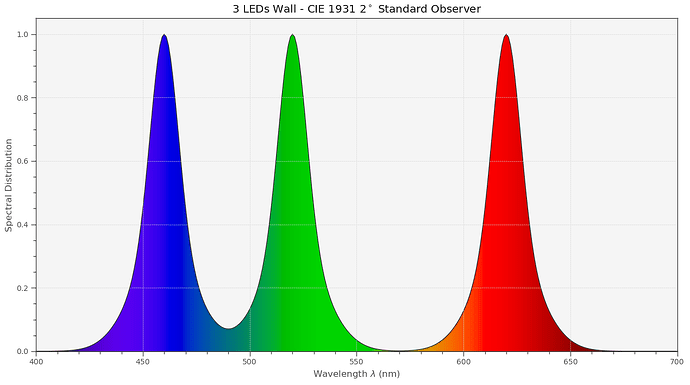
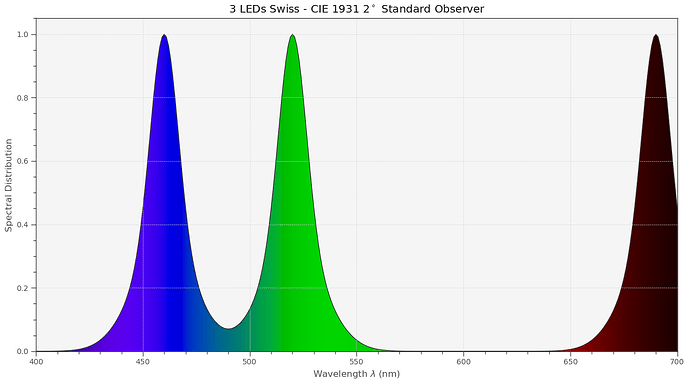
Before finishing, let’s look now how the spectrum of a narrowband RGB-LED setup would look like.
Specifically, I am using data from the Diastor paper “Investigation of Film Material - Scanner Interaction, Flueckiger et.al.”. The spectrum turns out to look like this:
Or, in comparison with the other spectra:
Note how far in the infrared region the Swiss red LED is sampling. Probably not a good idea. We will see soon…
So - this ends this post for today. As time permits, I will post more on this subject - including on how to simulate a camera by folding various spectra with each others. If somebody wants to read ahead, check this link (this page is talking about digital cameras and LED walls - a task very different from a scanner calibration, the one we are really interested in) and the ACES paper linked on this page at the bottom (I took this paper as a basis for computing the color science of the scientifc tuning file)